Heap

Heap 是一種 Data Structure ，要符合 Heap Condition (or Heap Property)
Heap property 是指 parent 和 children 的關係 (但 children 之間順序無關)

Min Heap : parent <= children
Max Heap : parent >= children

Heap 有一些不同的實作方法，如果只有寫 Heap，通常都是指 Binary Heap
其他種類如: Binomial Heap ， Fibonacci Heap ， Pairing Heap 等，參考 wiki Heap

(Binary) Heap

Heap 是一種 Binary Tree，不過要符合2個條件 :

外觀是 Complete Binary Tree
裡面元素都要符合 Heap Condition

雖然 Heap 在觀念上是一個 Complete Binary Tree ，但實際上是用 array 去 implement
這樣就能快速地去存取父(子)節點

node 的 index 是 i

parent : i / 2

left child : i * 2

right child : i * 2 + 1

Heap 的 push 為 O(log₂ N)，pop 為 O(log₂ N)

Priority Queue

Priority Queue 是一種 Abstract Data Structure，也是一種 container
當要從 Priority Queue 取出一個元素時，他會回傳最高優先度的元素並移除它
並可以 change 某元素之優先度，當然其位置也會改變

可以使用不同的 Data Structure 去 implement
舉一些例子 : [ search 表示搜尋時間，已知位置為 O(1)，否則為該 search 欄位時間 ]

	insert	remove	change	isEmpty	search
unsorted array	O(1)	O(n)	srch+O(1)	O(1)	O(n)
sorted array	O(n)	O(n)	O(n)	O(1)	O(log₂ n)
circular sorted array	O(n)	O(1)	O(n)	O(1)	O(log₂ n)
unsorted linked list	O(1)	O(n)	srch+O(1)	O(1)	O(n)
sorted linked list	O(n)	O(1)	O(n)	O(1)	O(n)
Binary Heap	O(log₂ n)	O(log₂ n)	O(log₂ n)	O(1)	O(log₂ n)

其中 Binary Heap 所花費的時間較為平均，O(1) < O(log₂ n) < O(n)
當然還有更快的作法，指示使用 Binary Tree 較為常見
有時也會稱 Priority Queue 為 Heap

快速建立 Binary Heap 或 PQ

假設要建立 Min Heap
給定一個隨機數值的 array ，將所有有 child 的 node (也就是subtree) 做 bulidMinHeap
直到所有subtree皆完成，就建立完成了

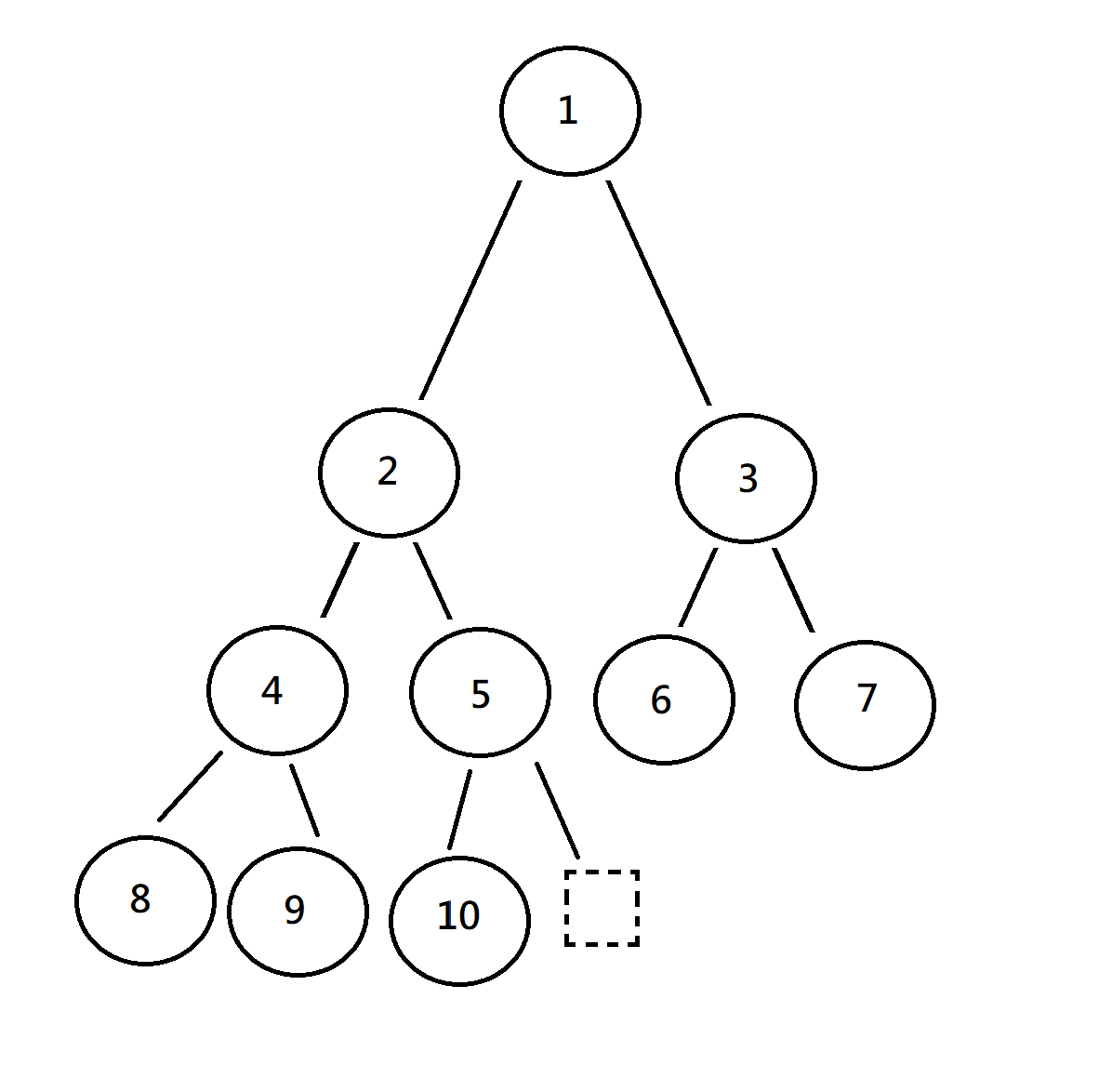
例如給定一個有 10 個 node 的 tree ，最後一個有 child 的 node 為 10/2 = 5
因此從 index=5 開始做 MinHeap
5 -> 4 -> 3 -> 2 -> 1
就完成了
費時 :

level 3 -> 耗時 1 (向下比較1次) * 2 個 = 2
level 2 -> 耗時 2 (向下比較2次) * 2 個 = 4
level 1 -> 耗時 3 (向下比較3次) * 1 個 = 3
total = 9

Genneral ( 廣義來說 ) : 共有 N 個元素

共有 log₂N+1 = k 層 (假設為 Full Binary Tree)
( M_i : 第 i 層有 $ \frac{N}{2^{k-i}} $ 個元素 )

level k-1 -> 耗時 : $ 1 \times M $_k-1 = $ 1 \times \frac{N}{2^1} $
level k-2 -> 耗時 : $ 2 \times M $_k-2 = $ 2 \times \frac{N}{2^2} $
level k-3 -> 耗時 : $ 3 \times M $_k-3 = $ 3 \times \frac{N}{2^3} $
                       。
                       。
                       。
level 1 -> 耗時 : $ (k-1) \times M $₁ = $ (k-1) \times \frac{N}{2^{k-1}} $

Total time = $ \sum\limits_{i=1}^{k-1}i \times \frac{N}{2^{k-i}} = \frac{N}{2} + \frac{2N}{4} + \frac{3N}{8} + \frac{4N}{16} …$

耗時 = O(N)

Binary Heap 實作

首先設一個依據 Heap property 比較大小的 function

// Min Heap
bool compare_with_heap_property(int a, int b) const
{
    return arr[a] < arr[b];
}

// Max Heap
bool compare_with_heap_property(int a, int b) const
{
    return arr[a] > arr[b];
}

然後在寫 heap_down(向下比較) 與 heap_up(向上比較)

void heap_down(int up)
{
    int down = up * 2;

    while (down <= nowSize)
    {
        if (down != nowSize && compare_with_heap_property(down + 1, down))
            ++down;

        if (compare_with_heap_property(down, up))
        {
            swap(down, up);
            up = down;
            down *= 2;
        }
        else
        {
            break;
        }
    }
}

void heap_up(int down)
{
    int up = down / 2;

    while (up >= 1)
    {
        if (compare_with_heap_property(down, up))
        {
            swap(down, up);
            down = up;
            up /= 2;
        }
        else
        {
            break;
        }
    }
}

接下來就可以去實作 快速建立Heap 、push(insert) 、pop(delete)

快速建立Heap

利用上方 #3 介紹的概念

void build(void)
{
    for (int up = nowSize / 2; up >= 1; --up)
        heap_down(up);
}

push(insert)

void push(const T &input, const int key = 0)
{
    if (nowSize == capacity)    // capacity is full
        extend_capacity();

    arr[++nowSize].setData(input);
    arr[nowSize].setKey(key);

    heap_up(nowSize);
}

pop(delete)

void pop(void)
{
    if (empty())
    {
        cerr << "no element" << endl;
        return;
    }

    arr[1] = arr[nowSize--];

    heap_down(1);
}

參考網站