UVa 10189 : Trouble of 13-Dots

Posted on | In |  
Symbols : 1.6k 字

有 N 種商品，每個價值為 Vi、喜愛程度為 Di，求金額不超過 M 的話，Dot 小姐可以獲得的最大喜愛點數總合。
此外，若實際購買金額超過 ( exeed ) 2000 的話，可以多獲得 200 的回饋
也就是若是購買了 5000 元，則就可以購買總額 5200 元。

測資(ㄧ)
Input :

500 4
100 2
100 3
200 3
400 4

Output :

8

測資(二)
Input :

1801 3
2000 3
1900 1
101 1
1801 3
2001 3
1900 1
101 1

Output :

2
3


核心思想

觀察一下，可以發現這題是 01 背包問題再加上一點變形。

我們來一步一步慢慢思考。

這題由題意來看，並不需要剛剛好把錢花完，因此在初始化紀錄動態規劃過程的陣列 val 時可以全部初始化為 0
代表無論最高花費金額為多少，0 點喜愛點數都是合法的。計算完後，解答就是 val[M]

反之，若條件是一定要剛好把錢花完，則要初始化為 -INFINITE (不合法狀態)，只有 val[0] = 0
因為只有 Value = 0 時是合法的，可以剛好取得 nothing，其他的 Value 皆為不合法

轉換方程式

從前 i 個商品中，總金額不超過 j 元的大最喜愛點數
val[i][j] = max(val[i-1][j], val[i-1][j-P[i]] + D[i])
或是縮減版的
val[j] = max(val[j], val[j - P[i]] + D[i])

解法引導

若不考慮可以額外加 200 元的這個 bonus，當最高花費金額為 M 時，最後答案就是 val[M]

再將此 bonus 加入考慮時，我們就要來探討一下尷尬的邊界範圍，也就是在 2000 附近

  1. M <= 2000 且 M + 200 <= 2000
    這種情況下因為不會觸碰到特殊規則，所以就是做完 01 背包問題後，解答為 val[M]
  2. M > 2000
    這種情況下最後的解答為 val[M + 200]
    因為若是最後購買的總合沒有用到 bonus ( 假設為 s 元且 s <= 2000 )，那麼解答 val[M + 200] = val[M] = val[s]
    若最後的購買總額 b > 2000，那麼 val[M + 200] = val[b]

  3. M <= 2000 且 M + 200 > 2000
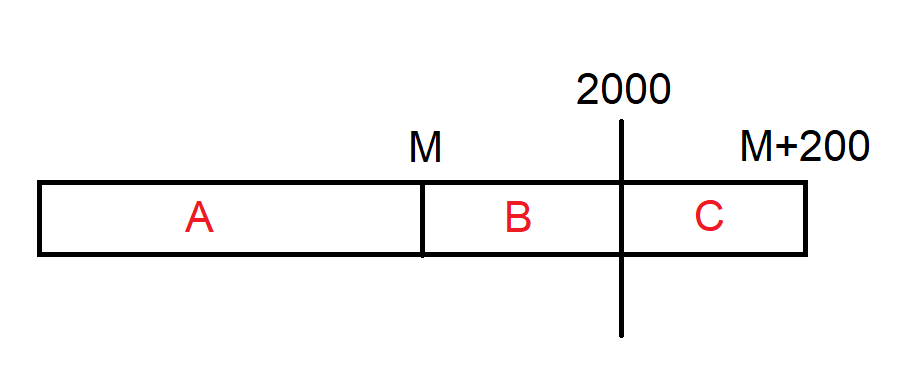    這種情況下整體的最佳解會落在以下 3 個區域

    • A 區域 : 不會碰到特殊規則，答案為 val[M]
    • B 區域 : 不合法地帶，因為購買金額超過了 M，但又沒有到達 2000，因此答案是 val[M]
    • C 區域 : 答案為 val[M + 200]

    那麼要如何知道最佳解會落在那裡呢?
    根據我們剛剛的前提，並不需要把錢都剛好花完
    所以假設 val[i] 剛好更新為在花費不超過 i 元的情況下所能得到的最大喜愛點數 Di
    且下一個更新點為 val[k] = Dk ( k > i )
    因此 val[i ~ k-1] 就皆會等於 Di，且 val[i] != val[i-1] 和 val[i] != val[k]
    所以我們可以從 M+200 開始往回掃描，分析當 val[i] != val[i - 1] 時

    • i >= 2001 : 最佳解在 C 區，答案為 val[M+200]
    • i <= 2000 且 i > M : 最佳解在 B 區，答案為 val[M]
    • i <= M : 最佳解在 A 區，答案為 val[M]

乍看之下，本題似乎已經解出來了呀 ~~ 收工!!
但不知道各位有沒有注意到，第三種情況的答案會出問題!!!

Why????

原因在於 : 若最佳解落在 B 區域，則會連帶地影響到 C 區域的最佳解

舉例來說，若實際上不含 B 區域的最佳解在 C 區域且為 20 ( 下圖 )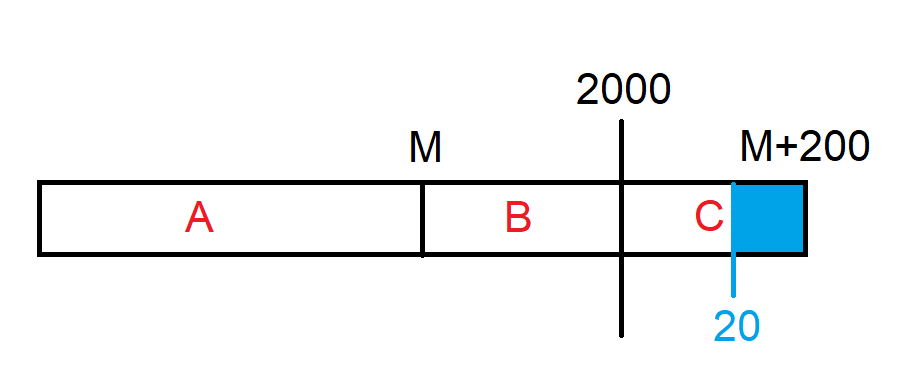

但是若又在 B 區域找更好的解答 ( 但實際上他是不合法的 )，他卻會把後面的真正解答蓋掉 ( 下圖 )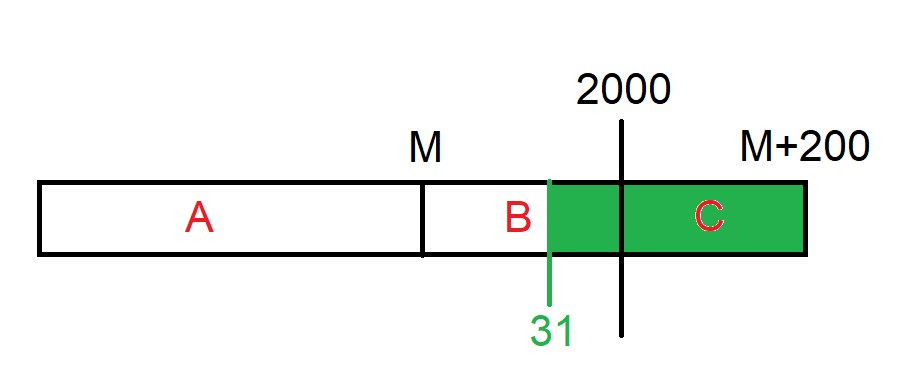

根據我們剛剛的演算法，當我們判斷出最佳解是落在 B 區域時
除非我們要在計算過程中去紀錄資訊，否則我們會沒辦法找回真正的解答

因此，我們需要修正我們的演算法

正確解法

可以發現，剛剛的問題是出在我們需要找的真正解答會被覆蓋掉
那麼我們就要想辦法去保留住他

一個很簡單的改變方式就是我們把我們剛剛的前提改一下
改成我們必須把錢剛好花完，因此在初始化 val 陣列時，只有 val[0] = 0，其餘皆為 -INFINITE ( 代表不合法 )

因此轉換方程式就要改為 :

若 val[j-P[i]] 有合法的最佳解，則選出最大的
if(val[j - P[i]] != -INFINITE) --> val[j] = max(val[j], val[j - P[i]] + D[i])

並同樣來分析一下 3 種情況

  1. M <= 2000 且 M + 200 <= 2000
    這種情況下因為不會觸碰到特殊規則，解答為 max( val[0] ~ val[M] )
  2. M > 2000
    解答為 max( val[0] ~ val[M + 200] )
  3. M <= 2000 且 M + 200 > 2000
    這種情況下整體的最佳解就是從 A 和 C 區域中去挑選

改良過後，每一個合法解都會被保留住，最後只需要判斷出範圍並找出最大值就好

程式碼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

class Solution
{
public:
	Solution()
	{
		ios::sync_with_stdio(false);
		cin.tie(nullptr);
		cout.tie(nullptr);
	}

	int calculate(const vector<pair<int, int>> &items, const int M)
	{
		const int Money = M + 200;

		val.clear();
		val.resize(Money + 1, -1000000);
		val[0] = 0;

		int i, k;

		for (i = 0; i < items.size(); ++i)
			for (k = Money; k >= items[i].first; --k)
				if (val[k - items[i].first] >= 0)	// if has valid answer
					val[k] = max(val[k], val[k - items[i].first] + items[i].second);

		int m = -1;

		if (M <= 2000)
			m = max(find_max(0, M), find_max(2001, Money));
		else
			m = find_max(0, Money);

		return m;
	}

private:
	vector<int> val;

	int find_max(int start, int end) const
	{
		int max = 0;

		for (int i = start; i <= end; ++i)
			if (val[i] > max)
				max = val[i];

		return max;
	}
};

int main(void)
{
	int money, items_n;
	int price, idx;
	int ans;
	Solution s;

	vector<pair<int, int>> items(100);

	while (cin >> money)
	{
		cin >> items_n;

		items.clear();

		while (items_n--)
		{
			cin >> price >> idx;

			items.emplace_back(price, idx);
		}

		ans = s.calculate(items, money);

		cout << ans << endl;
	}

	return 0;
}


UVa 真實測資

以下我偷渡出來的 UVa 測資和我的程式 run 的解答，請低調享用

  1. UVa 10819 Test Data
  2. My Ans
0%