Segment Tree

當需要大量對 array 中給定範圍做諮詢，並且也會大量的做某些值的修改時，我們就可以使用線段數 ( Segment Tree )
此外，針對範圍查詢或是值的修改，我們也可以使用其他的資料結構或方法，以下為比較表格

—-	Query a range	change a value	資料結構適用條件
一般陣列	O(N)	O(1)	少量查詢，大量修改
Prefix Sum Array	O(1)	O(N)	大量查詢，少量修改
Segment Tree	O(logN)	O(logN)	大量查詢，大量修改

甚麼是 Segment Tree

假設有一陣列 A 共有 N 個元素，可以建構出一棵線段數 T，其中

T 的 leaf node 代表陣列 A 中的一個元素 A[i] , 1 <= i <= N
T 的 internal nodes 代表陣列 A 中一個範圍內所有元素的集合 A[i : k] , 1 <= i < k <= N
T 的 root 代表陣列 A 所有元素的集合 A[1 : N]

因此，因為 T 的 root 所代表的範圍是 1 ~ N，所以他的 2 個 children 代表的範圍分別為 [1 ~ M] 和 [M+1 ~ N] ( M = (1+N)/2)
一直使用二分法去 build，所以 Segment Tree 的樹高為 $ ceil({ \log_2 N }) $
此外，由於 Segment Tree 是 binary tree，因此 internal node 為 N - 1 個，總節點數為 2*N - 1

例如下圖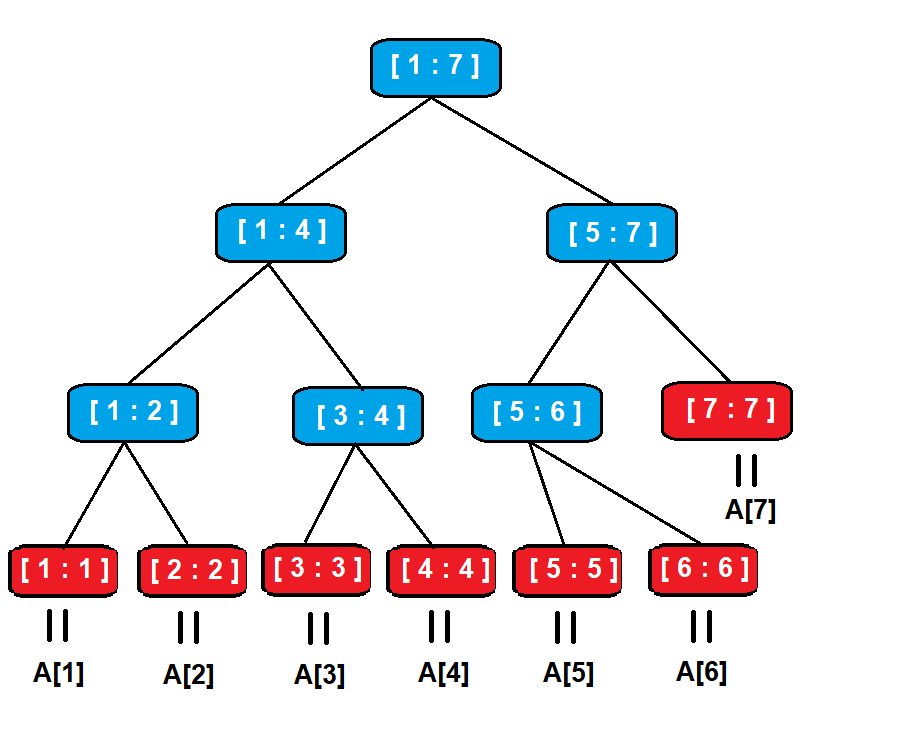

藍色為 internal nodes，紅色為 leaves，中間為他們所代表的 array 範圍，且 leaf 就會等於 array 中單一元素的值

操作

Segment Tree 有 2 種操作 :

Update : 將 Array A 的某個元素更新，並且要修正相對應的 Segment Tree
Query : 利用 segment tree 獲取指定 array 範圍的資訊。例如求最大值、最小值、元素總和或是其他的操作

實作

我們可以使用一維陣列來實現 Segment Tree，就像是 Heap 一樣，若 parent 的 index 為 i
則左子樹為 i * 2 且右子樹為 i*2 + 1 ，注意 index 是從 1 開始

那我們要將存甚麼資料在 Tree Node 中呢 ?
這就取決於你要用線段樹來做甚麼操作，若是求線段總和，那就要存該 range 的總和。若是求最大值，則要存的是區間中的最大值
而對於線段樹的操作 ( build tree、update、query )，我們都可以使用 recursive 的方式去達成

例如下圖為有 7 個元素的 array 所建出來的線段樹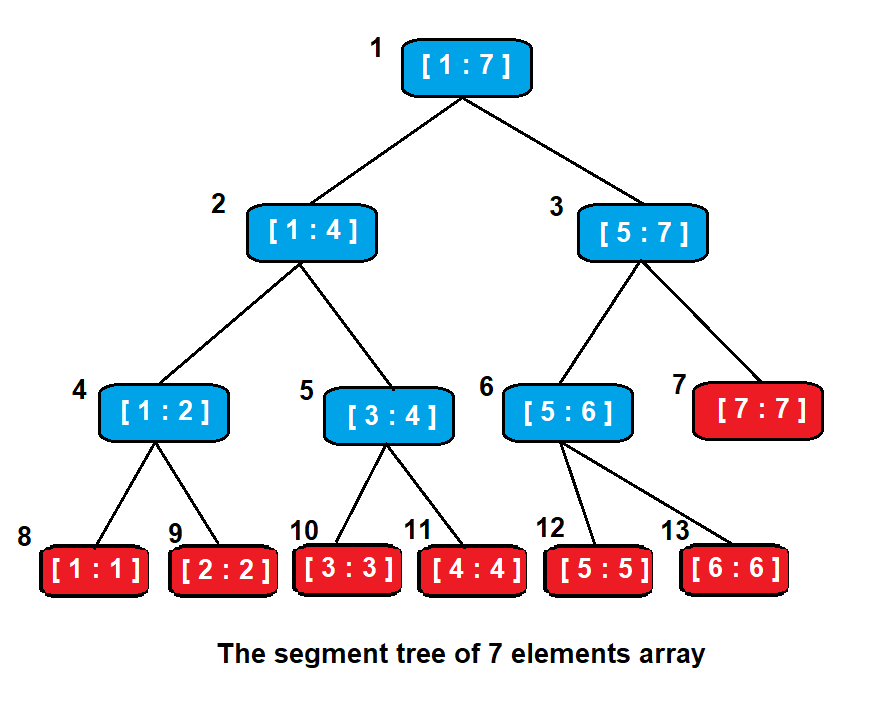

用一為陣列來表示

Index	1	2	3	4	5	6	7	8	9	10	11	12	13
Tree	A[1:7]	A[1:4]	A[5:7]	A[1:2]	A[3:4]	A[5:6]	A[7]	A[1]	A[2]	A[3]	A[4]	A[5]	A[6]

接下來我們用計算總合的 segment tree 來說明

Build Tree (bottom-up approach)

首先，我們要先知道 segment tree 的 array 大小，若 data array 的大小為 N
先算出樹高 h = $ { \log_2 N } $，在算出此高度全滿所需要的 node 個數為 $ { 2^{h+1} } $
( 注意 index 從 1 開始 )

void initial(void)
{
	double h = log2(size);
	h = ceil(h) + 1;
	int tree_size = static_cast<int>(pow(2, h)) - 1;

	tree.clear();
	tree.resize(tree_size + 1);
}

接下來就是要 build tree

int build(int root_idx, int range_start, int range_end)
{
	if (range_start == range_end)
	{
		tree[root_idx] = data[range_start];
		return tree[root_idx];
	}

	int mid = get_mid(range_start, range_end);

	int lv = build(root_idx * 2, range_start, mid);
	int rv = build(root_idx * 2 + 1, mid + 1, range_end);

	tree[root_idx] = lv + rv;

	return tree[root_idx];
}

若 start == end ，代表此為 leaf node
否則就遞迴求出左子樹與右子樹的值並相加

由於要建立每一個節點，因此 Build 耗時 $ O(N) $

Update

要去判別要更新的點是屬於左子樹的範圍還是右子樹的範圍
並且更新的值我們要用差 ( difference ) 去計算

void update(int index, int val)
{
	if (index < 1 || index > size)
		return;

	if (data[index] == val)
		return;

	_update(1, 1, size, index, val - data[index]);
}

void _update(int root_idx, int range_start, int range_end, int data_idx, int dif)
{
	if (range_start == range_end)
	{
		data[data_idx] += dif;
		tree[root_idx] += dif;

		return;
	}

	int mid = get_mid(range_start, range_end);

	if (data_idx <= mid)
		_update(root_idx * 2, range_start, mid, data_idx, dif);
	else
		_update(root_idx * 2 + 1, mid + 1, range_end, data_idx, dif);

	tree[root_idx] = tree[root_idx * 2] + tree[root_idx * 2 + 1];
}

update 類似於二分搜尋，因此耗時 $ O({log_2 N}) $

Query

對於要查找的範圍 R 與目前正在查找的 node 範圍 P 可以分成 3 種情況 :

若 node 範圍 P 完全包含於範圍 R 中，則直接回傳該 node 值
若 node 範圍 P 完全不在範圍 R 中，則回傳一個不改變計算結果的值 ( 若是算總和，則是 0，因為 X+0=X)
若 node 範圍 P 有部分在範圍 R 中，部分在 R 外面，則將 P 分割成左右部分繼續遞迴呼叫，並相加其結果

int query(int l_idx, int r_idx) const
{
	return _query(1, 1, size, l_idx, r_idx);
}

int _query(int root_idx, int range_start, int range_end, int l_idx, int r_idx) const
{
	// the range of this node is completely in the searching range
	if (l_idx <= range_start && range_end <= r_idx)
	{
		return tree[root_idx];
	}

	// the range of this node is completely out of the searching range
	if (range_end < l_idx || range_start > r_idx)
	{
		// return the value which will not affect the answer after adding it
		return 0;
	}

	// the range of this node is partially in the searching range and partially out of the searching range

	int mid = get_mid(range_start, range_end);
	int lv = _query(root_idx * 2, range_start, mid, l_idx, r_idx);
	int rv = _query(root_idx * 2 + 1, mid + 1, range_end, l_idx, r_idx);

	return lv + rv;
}

同樣地是類似於二分搜尋法，因此 Query 耗時 $ O({log_2 N}) $

甚麼是 Segment Tree

操作

實作

Build Tree (bottom-up approach)

Update

Query

參考